In this article we’ll consider the last of the initial set of measurements, the column plate-number, N. This is also called the column efficiency, and is calculated as
N = 16 (t R / wb)2
where wb is the column width at baseline between tangents drawn to the sides of the peak, as in Figure 1. An alternate way to calculate N is to use the peak width at half the peak height, w0.5:
N = 5.54 (t R / w0.5)2
The half-height method is easier to determine directly from the computer monitor, because you don’t have to draw tangents. It also enables determination of N if the peak is not fully separated from a neighbouring peak, as long as the valley between the peaks is lower than the half-height. Half-height measurements commonly are the method of choice for automatic determination of N by data systems.
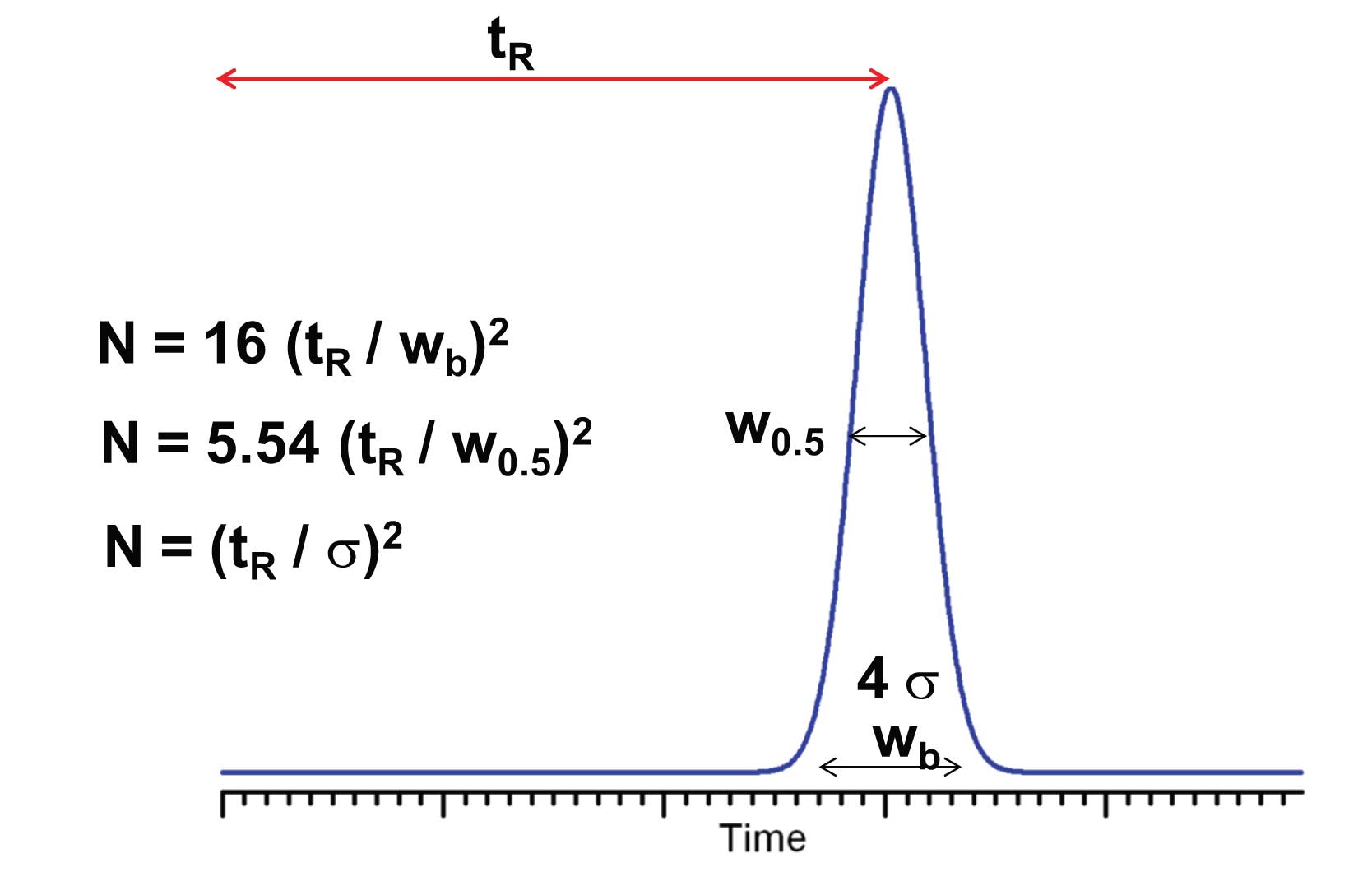 Figure 1
Figure 1
You might wonder what the plate number represents. In a convoluted way, it is related to distillation technology, where a distillation column can have different stages, or plates, but the best spinning-band distillation columns may have only a hundred or so plates, whereas even a poor HPLC column will generate thousands of plates. So relating N to distillation is a stretch. And it is not the number of plates in the buffet line at the local restaurant – in fact, I think that number commonly is (n-1), because the person in front of me just took the last plate!
On a more serious note, the plate number can be related to the statistical broadening of a peak. Recall from your basic statistics class that tangents drawn to the sides of a Gaussian distribution intersect the baseline at ±2 standard deviations (σ). A well-behaved chromatographic peak should be Gaussian in shape, so we can conclude that the peak width at baseline is 4σ. If you substitute 4σ for wb in the first equation, you’ll see that N is merely the square of the retention time divided by
N = (t R / σ)2
Now with that and a couple of dollars, you can buy a cup of coffee at the local coffee shop – aren’t you glad you asked?
So What?
What is so great about N? Why not just use the peak width to describe a peak? The beauty of the column plate-number from a practical standpoint is that it is approximately the same for all peaks in a chromatogram. And N is possible to calculate from first principles, so we can get a good idea of what N should be for a given column, mobile phase, temperature, and solute without doing the actual experiment. And while this is not accurate enough to make exact comparisons, it allows us to evaluate whether or not the plate number obtained from a given column is reasonable for the conditions. Plate numbers that are lower than expected, say by 30% or more, may be the result of column aging, unwanted chemical effects, poor system plumbing, or other problems. In future ‘HPLC Solutions’ discussions, we’ll look at how
N can be combined with k and α to evaluate resolution during method development.
I’ll end with a cautionary note – calculation of N, as in equations 1 and 2 is only possible for isocratic separations. This technique is not appropriate for gradients – it is best just to use peak width to describe gradient peaks.
This blog article series is produced in collaboration with John Dolan, best known as one of the world’s foremost HPLC troubleshooting authorities. He is also known for his research with Lloyd Snyder, which resulted in more than 100 technical publications and three books. If you have any questions about this article send them to TechTips@sepscience.com




