In the previous article we began our study of the fundamental resolution equation
Rs = ¼ (N)0.5 (α-1) (k / [1+k]) (1)
Where N is the column plate number or efficiency, α is the selectivity, and k is the retention factor. We saw that, because N contributes to resolution as a square-root function, using N by itself is not a very powerful approach to make large increases in resolution, such as by twofold or greater.
If we are going to use equation 1 as a guide for method development, we first need to pick a starting place. This means that we have to choose a column. If we plot the dependence of resolution on N, we can obtain the relationship shown in Figure 1. Here I have marked an N = 10,000 plate column as a recommended starting point. This is a 100 x 4.6 mm, 3 µm or 150 x 4.6 mm, 5 µm column. Either of these columns can be run at 2 mL/min, so the run times will not be excessive. And they have sufficient peak capacity to separate approximately 12 sample components without a huge challenge. If we choose a 250 x 4.6 mm, 5 µm column, we gain only ≈30% in resolution for a 65% increase in retention time and pressure – not a very good tradeoff. If we want to maintain the original pressure, we would have to make a corresponding reduction in flow rate, further increasing the run time – even less desirable. In contrast, if we are doing LC-MS, the detector has separation power that complements that of the chromatographic column, so we usually choose a 50 x 4.6 mm, 3 µm column that generates N ≈ 5000. This generally is sufficient for LC-MS applications and allows shorter run times than a 100 or 150 mm long column.
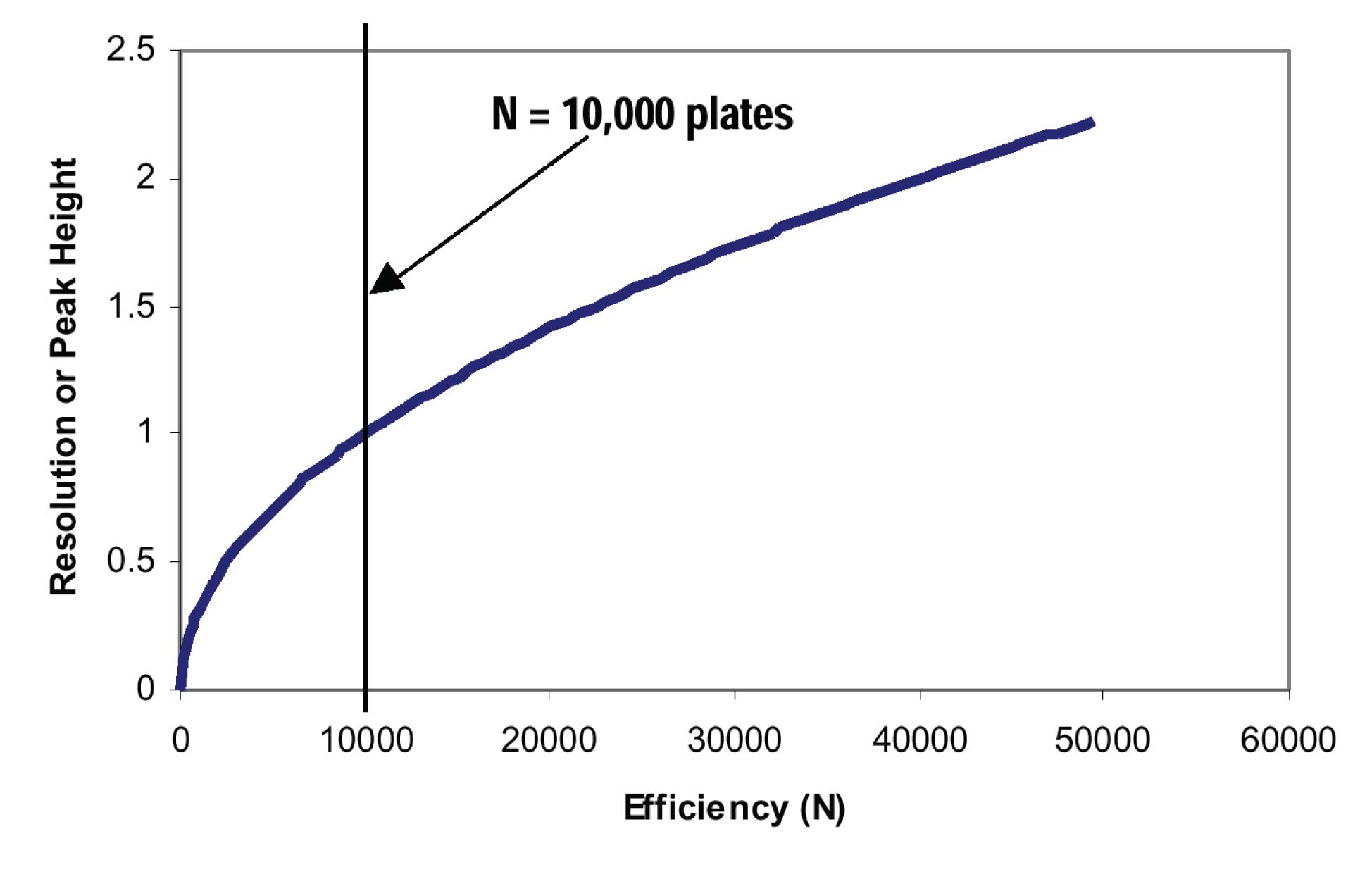 Figure 1
Figure 1
What about the use of sub-2-µm particles as a means to increase N and thus resolution? The plate number is inversely related to particle size, so a change from 5 µm to 2 µm particles would give a 5/2 or 2.5-fold increase in N. But this would increase resolution only by (2.5)0.5≈ 1.6-fold. This doesn’t seem too bad until we consider the relationship between particle size and pressure. Pressure increases inversely with the square of the particle size change. That is, the 2.5-fold reduction in particle size would generate a 6.25-fold increase in pressure. A 150 x 4.6 mm column operating at 2000 psi (140 bar) with 5 µm particles would generate 12,500 psi (860 bar) if it were filled with 2 µm particles. This would require either the purchase of a higher-pressure HPLC system or reduction of the flow rate by >2-fold (with a corresponding increase in run time) to keep the pressure within the operating limits of a conventional HPLC system. Of course, a shorter (e.g., 100 mm) 2 µm column might be an acceptable compromise for a smaller gain in resolution with a smaller penalty in pressure.
The bottom line is that the plate number is not a very powerful way to leverage resolution because of the square-root dependence of Rs on N. It is best to pick a column that is likely to separate the complexity of sample you are using and then take advantage of k and α for changes in selectivity to increase Rs. For most of us, this means a 150 x 4.6 mm, 5 µm or 100 x 4.6 mm, 3 µm column operated at 1-2 mL/min.
This blog article series is produced in collaboration with John Dolan, best known as one of the world’s foremost HPLC troubleshooting authorities. He is also known for his research with Lloyd Snyder, which resulted in more than 100 technical publications and three books. If you have any questions about this article send them to TechTips@sepscience.com




