A reader recently asked how to determine the column volume of a column packed with superficially porous particles. You’ll recall that these are a newer type of HPLC packing material, variously referred to as superficially porous, core-shell, fused-core, shell-type, pellicular, or some other name to describe the fact that the particle comprises a solid center (core) covered by a porous layer of silica, where the chromatography takes place. Figure 1 is a sketch comparing a traditional, fully porous particle with a superficially porous one.
Estimating the column volume is not difficult if we make a few assumptions. The first of these is that a column packed with fully porous particles has a total column porosity of about 60%. In other words, 60% of the column is filled with mobile phase and 40% is occupied by the silica particles. From this, we can derive a simple formula to estimate the volume of a fully porous particle column:
VM = 0.5 x 10-3 L dc2 (1)
where VM is the column volume (in mL), L is the column length (in mm), and dc is the column internal diameter (also mm). This should be good within ±10%. So, for example, a 150 x 4.6 mm column would give VM≈ 1.6 mL.
Our next assumption is that about half of the mobile phase is inside the particles and half is between the particles. With either type of particle, we’ll assume that the packing technology is identical, so the space between the particles will be the same. This means that any difference in VM will be due to the amount of solvent inside the particles. One of the popular superficially porous particles has a 1.7 µm diameter core with an 0.5 µm thick shell for a 2.7 µm total diameter. Using the formula for the volume of a sphere (V = 4/3 Π r3), we can calculate that 75% of the volume of the superficially porous particle is in the shell and 25% in the core (other superficially porous products may have different ratios). This means that a comparable sized fully porous particle would have about 25% more pore volume. Since this difference in volume only applies for the intra-particle volume, which is about half of the total column volume, it would reduce the total column volume by half of this amount (25%/2 = 12.5%). This suggests that the estimate of VM obtained from equation (1) should be reduced by 12.5% for superficially porous particles.
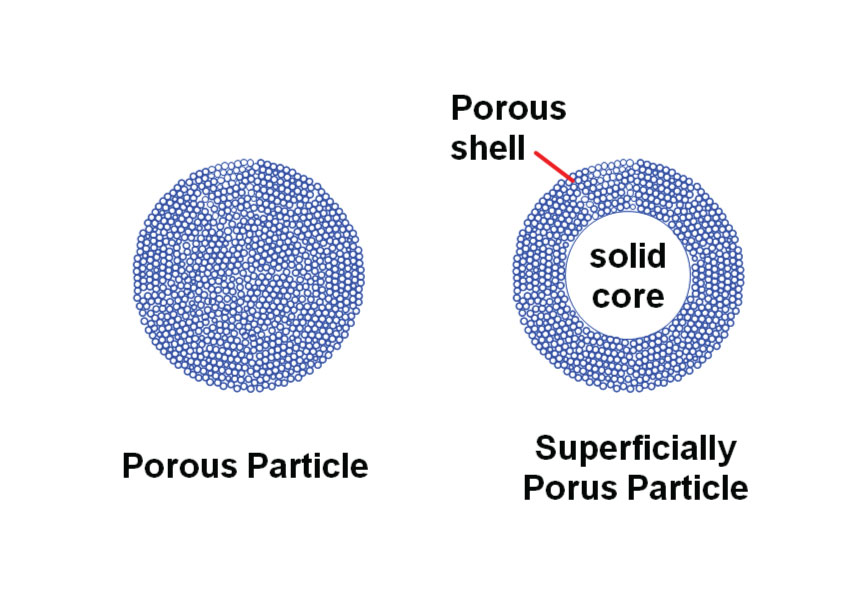
Figure 1
So what does all this mean? You can see that I’ve piled assumption upon assumption in making the estimates of VM, so these numbers should be taken for what they are – estimates. A better value of VM can be obtained by measuring it from a chromatogram with a marker such as uracil or thiourea. But we can see that it is reasonable to expect VM to be 10-15% less with a superficially porous particle than for a comparable column packed with fully porous particles.
This blog article series is produced in collaboration with John Dolan, best known as one of the world’s foremost HPLC troubleshooting authorities. He is also known for his research with Lloyd Snyder, which resulted in more than 100 technical publications and three books. If you have any questions about this article send them to TechTips@sepscience.com




