A reader wrote to ask why he was seeing such a difference in the appearance of a gradient chromatogram when all he did was change the flow rate. He’d been making similar changes with isocratic methods for years – an increase in the flow rate shortened the run time, but had little other impact on the separation. Let’s take a look at what is going on here.
First, recall that the isocratic retention factor, k, is unaffected by flow rate. The k-value is calculated as:
k = (t R – t 0) / t 0 [1]
where t R and t 0 are the retention time and the column dead-time, respectively. The dead time is estimated from the first rise in the baseline at the garbage peak or solvent front at the first of the chromatogram. Multiply the dead time by the flow rate, F, and you’ll get the column volume, V M = t 0 F. Note that if you increase the flow rate by two-fold, both t R and t 0 in equation 1 are reduced by twofold, but k stays constant. If k is changed, as by changing t R but not t 0, it is unlikely that it will change for all components of the sample in exactly the same way, and a change in peak spacing often occurs.
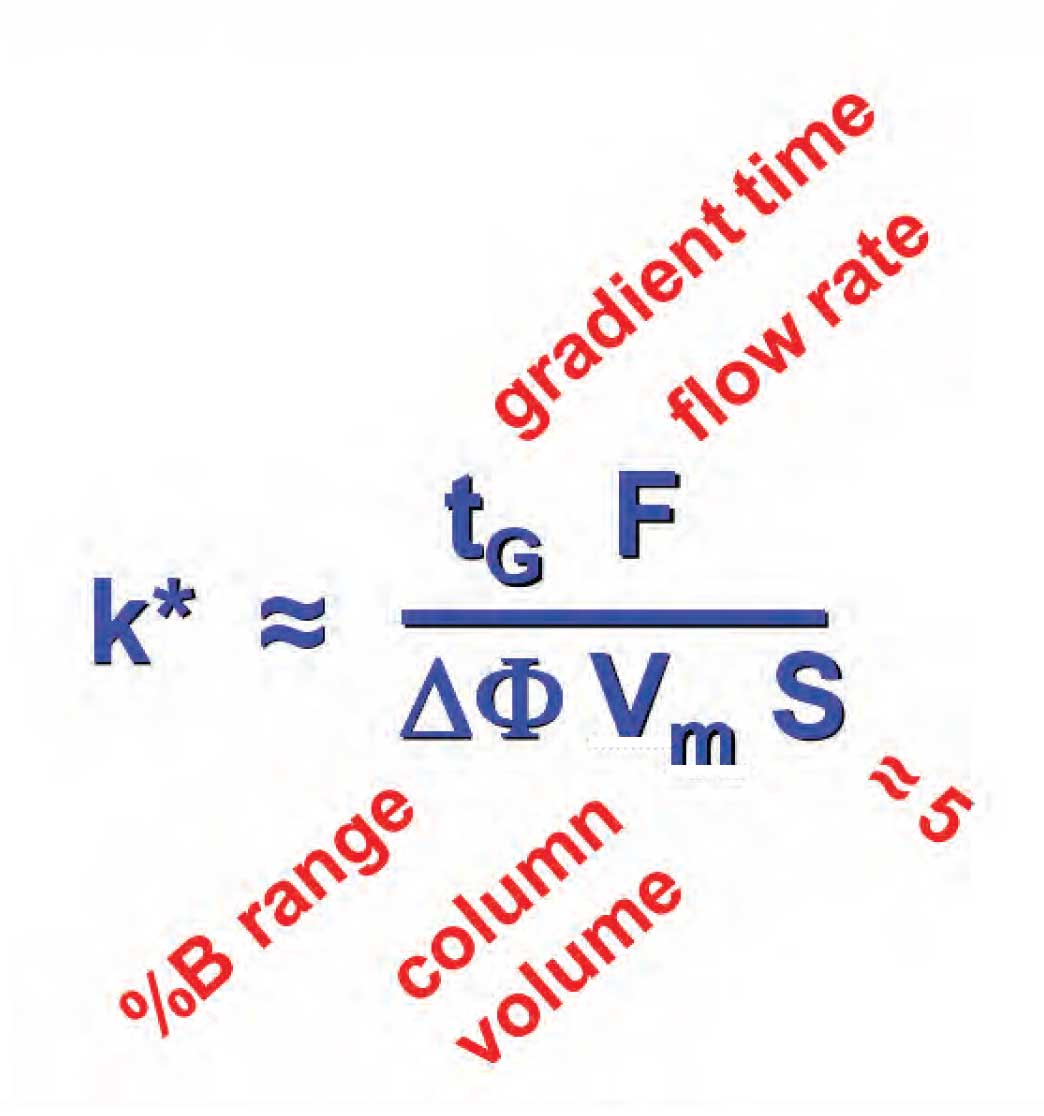 Figure 1
Figure 1
The same principle holds for gradient elution. If we change conditions that change the gradient retention factor, k* , a change in peak spacing often occurs, but if k* is kept constant, no change in peak spacing will happen. Unlike isocratic k expressed in equation 1, gradient k* is a bit more complex, as shown in the equation in Figure 1. You can see that it comprises a function of gradient time, t G, flow rate, gradient range, ∆%B, column volume, and the S-value. The gradient range is expressed as a decimal, for example, a gradient of 5-80%B gives ∆%B = 0.75. S is the slope of the isocratic log k vs. %B (%-organic solvent) plot, and is constant for a given compound. A value of S ≈ 5 can be used as an estimate for compounds of molecular weight Now that we are armed with the equation of Figure 1, we can see where the reader got in trouble. An increase in the flow rate by a factor of two will likely shorten the run time, but it also changes k* by a factor of two. And just as with isocratic k , a twofold change in k* is not likely to be exactly the same change for all compounds in the sample. When k* is changed, a change in the peak spacing is expected, and should not come as a surprise. The way to keep the peak spacing constant is to change another factor in Figure 1 to compensate. For example, increase F by a factor of two and decrease t G by the same amount, thus keeping k* constant and the peak spacing constant. The same procedure holds for changes in the gradient range and column size.
This blog article series is produced in collaboration with John Dolan, best known as one of the world’s foremost HPLC troubleshooting authorities. He is also known for his research with Lloyd Snyder, which resulted in more than 100 technical publications and three books. If you have any questions about this article send them to TechTips@sepscience.com




