I recently had an email from a reader who wondered how it was possible to use an evaporative light scattering detector (ELSD) with an HPLC for quantitative analysis when instead of a linear response, the concentration vs response relationship behaves more closely to a power curve.
For key concepts in the performance of HPLC methods, I consider the International Committee on Harmonization (ICH) documents a good resource. In this case, ICH Q2(R1) [1] is the document to consider (these documents are available for free on the FDA website). In the Glossary of [1], item #7 defines linearity as:
“The linearity of an analytical procedure is its ability (within a given range) to obtain test results which are directly proportional to the concentration (amount) of analyte in the sample.”
Then in Section II, item #2 further discusses linearity:
“A linear relationship should be evaluated across the range ... of the analytical procedure.... Linearity should be evaluated by visual inspection of a plot of signals as a function of analyte concentration or content. If there is a linear relationship, test results should be evaluated by appropriate statistical methods, for example, by calculation of a regression line by the method of least squares. In some cases, to obtain linearity between assays and sample concentrations, the test data may need to be subjected to a mathematical transformation prior to the regression analysis.... In addition, an analysis of the deviation of the actual data points from the regression line may also be helpful for evaluating linearity.... Some analytical procedures, such as immunoassays, do not demonstrate linearity after any transformation. In this case, the analytical response should be described by an appropriate function of the concentration (amount) of an analyte in a sample. “
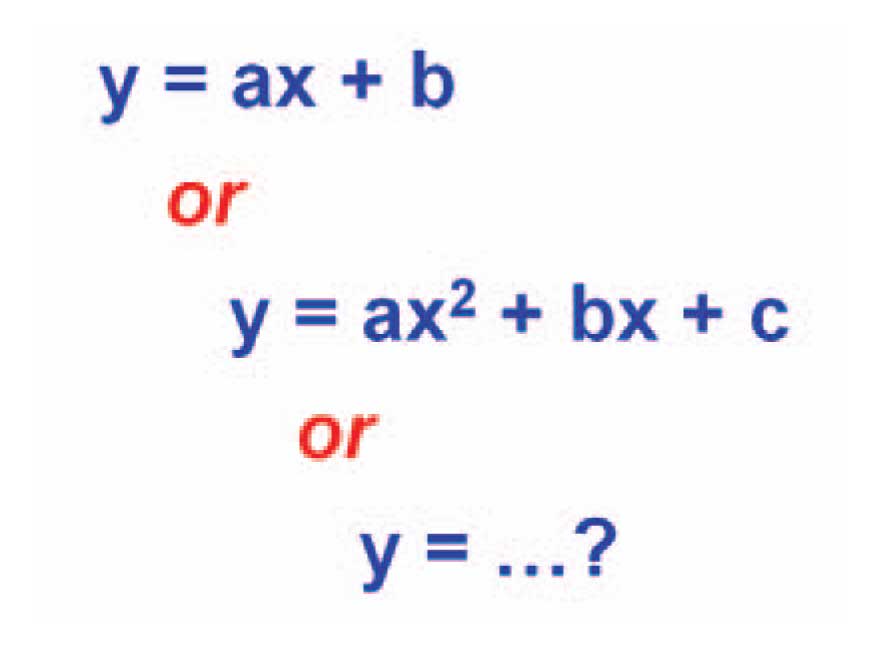
Evaluation
Let’s unpack these statements and see how to interpret them. (Be aware that these are my opinions and not official opinions of the regulatory agencies.) First, there needs to be a relationship from which you can determine the concentration of analyte based on the chromatographic response (peak height or area). Second, it also suggests that the response relationship often is best evaluated by visual examination of a plot of response vs concentration.
Third, once a relationship is determined, you should use statistical techniques to evaluate the performance of the calibration curve. The most common technique, of course, is to use a linear least-squares regression, evaluating the coefficient of determination, r2, as a measure of the quality of the fit.
Data Transformation
The ICH goes on to imply, however, that not all concentration vs response relationships are linear. That is, a mathematical transformation of the data may be required to obtain a satisfactorily linear relationship. Unfortunately, r2 is not always the best tool to use to evaluate linearity. This is because r2 is intended for data which have constant standard deviations throughout the concentration range; most chromatographic data have a constant relative standard deviation, rather than standard deviation, and other methods of data evaluation may be more meaningful. The ICH also allows for this, where the evaluation of the deviation of the actual data points from the regression line is used.
Which Technique to Use?
So which technique do we use to establish linearity for our method? The United States Food and Drug Administration [2] has some good advice to help us make the decision:
“Standard curve fitting is determined by applying the simplest model that adequately describes the concentration-response relationship using appropriate weighting and statistical tests for goodness of fit.”
To me this says that we should try the simplest curve-fit first, and resort to more complex transformations only if the simple fit is not adequate. For example, ultraviolet (UV) detectors used with HPLC behave linearly over several orders of magnitude in concentration, so a truly linear (y = ax + b) fit is expected. Other detectors, such as the ELSD mentioned above, or LC-MS, are known to be non-linear, so some kind of transformation will be needed to obtain the best concentration vs response relationship. And in some cases, it will not be possible to obtain a linear relationship with any transformation, as is suggested by the last two sentences in the ICH quote above. In such cases, you just have to do the best you can and try to build a solid case to support whatever technique you decide to use for calibration.
References
1. International Committee on Harmonization, “Validation of Analytical Procedures: Text and Methodology,” Q2(R1), Nov. 2005.
2. United States Food and Drug Administration, “Guidance for Industry: Bioanalytical Method Validation,” , May 2001.
This blog article series is produced in collaboration with John Dolan, best known as one of the world’s foremost HPLC troubleshooting authorities. He is also known for his research with Lloyd Snyder, which resulted in more than 100 technical publications and three books. If you have any questions about this article send them to TechTips@sepscience.com




