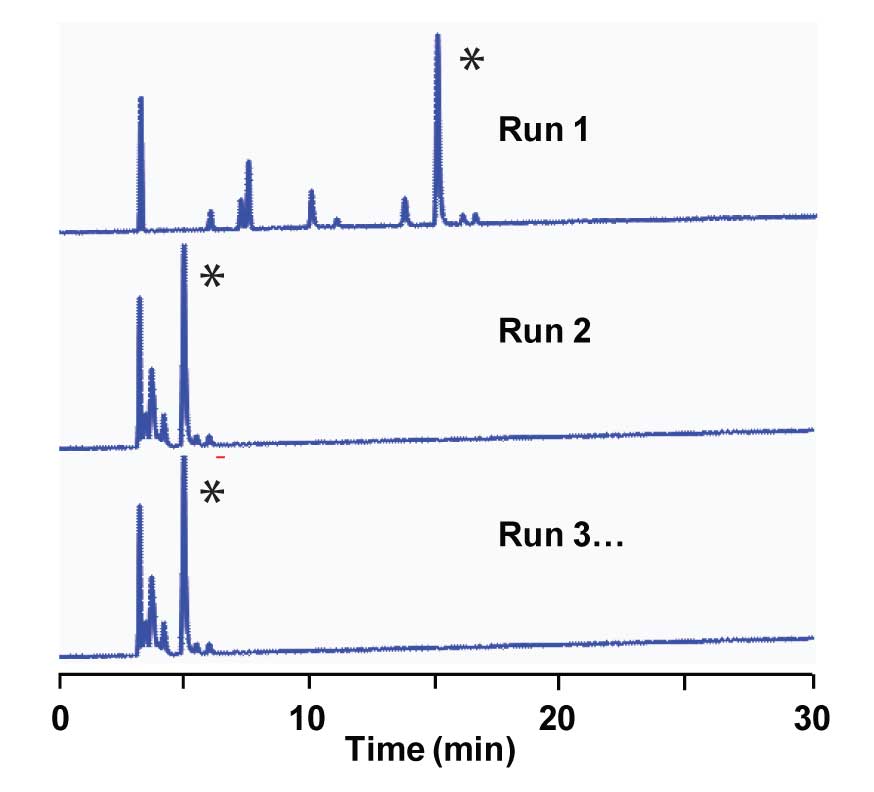
In a previous article (Poor Equilibration) we looked at a problem gradient method where peaks in the second and subsequent chromatograms were eluted too early. Our conclusion was that the most likely cause was insufficient equilibration time between runs. However, I also suggested that we make a quick check to see if the gradient conditions are reasonable, and this is even more important now that we’ve already discovered one problem with the method.
Recall the gradient conditions: The sample is a peptide (2675 Da) being analyzed on a 150 x 2.1 mm, 3 µm particle column by LC-MS using an ion trap MS in the positive electrospray ionization (ESI) mode. The A-solvent is 10% acetonitrile (ACN) in 0.1% trifluoroacetic acid (TFA); B is 100% ACN with 0.1% TFA added. The gradient runs from 0-100% B over 30 min, then steps back to 100% A for 20 min prior to the next injection. When the method is working properly, the retention time is ≈ 15 min.
Check the Gradient Conditions
Recall that with isocratic separations, we like to have the retention factor, k , in the 2 < k < 10 region for the best chromatographic behavior. The gradient retention factor, k *, is calculated a bit differently, but the same guidelines for 2 < k * < 10 apply. Let’s see what k * is for this method. We use
k * ≈ (t G F) / (∆%B V M S) [1]
where t G is the gradient time in min, F is the flow rate in mL/min, ∆%B is the gradient range (as a decimal; e.g., 15% B = 0.15), V M is the column volume in mL, and S is a constant for an individual compound, estimated as
S ≈ 0.25 √(MW) [2]
where MW is the molecular weight of the analyte. In the present example, S ≈ 0.25 √(2675) = 12.9. Last week we estimated V M = 0.33 mL. Now we can calculate
k * ≈ (30 x 0.1) / (0.9 x 0.33 x 12.9) = 0.8
So we can see that k * is smaller than is desirable, and because it is a single peptide being analyzed (the other peaks are of no interest as long as they are separated from the target analyte), there should be little reason not to change the conditions so that k * is in the desired range. For example, a change in the flow rate from 0.1 to 0.5 mL/min would increase k * to about 4, which is more reasonable. Also, based on the conclusions from last week’s discussion, this increase in flow rate would increase the equilibration volume between runs, likely solving the retention reproducibility problem.
This blog article series is produced in collaboration with John Dolan, best known as one of the world’s foremost HPLC troubleshooting authorities. He is also known for his research with Lloyd Snyder, which resulted in more than 100 technical publications and three books. If you have any questions about this article send them to TechTips@sepscience.com




